causal-inference-on-time-series-with-causal-impact
Notes: CausalImpact
Notes related to Causal Inference with CausalImpact, R Package from Google.
Why Causal Inference?
Let’s say we made changes to a policy, tool, campaign, or process we are
running. We may want to answer the question of what effect did change
X have on our service? The gold standard for estimating this effect is
a randomized control trial. However, that
might be too difficult, too expensive, unethical, or simply because it
wasn’t done. Causal inference is a technique designed to help estimate
the impact of a change in cases where a randomized experiment is not an
option.
A simple example
On January 15, 2015, the Swiss National Bank (SNB) announced it would
no longer hold the Swiss franc at a fixed exchange rate with the
euro.
The image below shows the exchange rate before the announcement, the
observed value after treatment (Y(1)) and the expected exchange rate
if no announcement had been made (i.e., the counterfactual
example Y(0)).
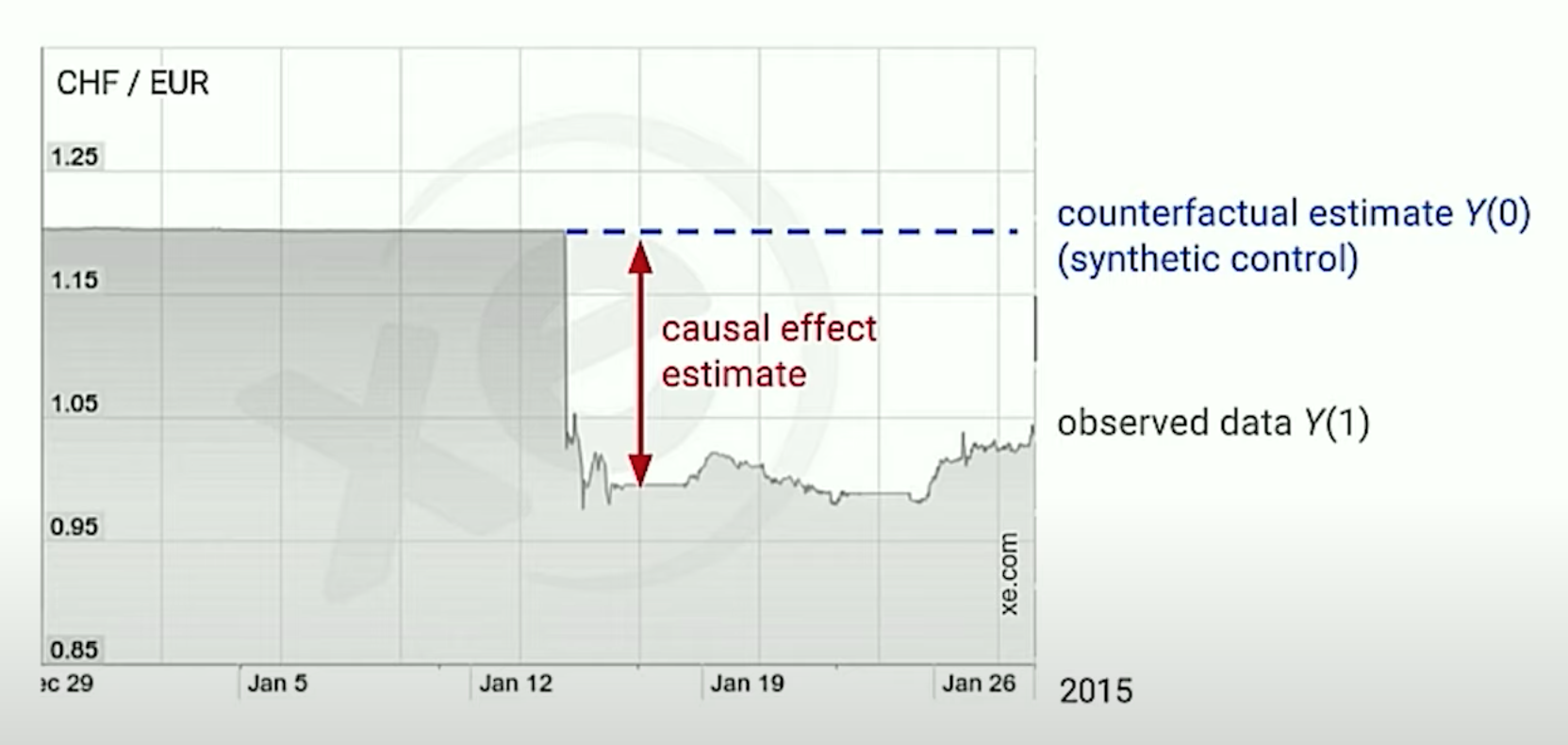 Source: Youtube - Inferring the effect of an event using CausalImpact
by Kay Brodersen
Source: Youtube - Inferring the effect of an event using CausalImpact
by Kay Brodersen
Key concepts in this image are:
Y(1)is our observed data, what actually happened after the treatmentY(0)is our counterfactual estimate, or synthetic control, or the expected outcome with no treatmentthe causal effect estimateis the difference between the observedY(1)and the synthetic controlY(O), or the difference between the two outcomes.
The problem of causal inference
We cannot observe the potential outcomes with and without the treatment at the same time. For instance, we cannot see a single patient’s outcome if we administered and did not administer a drug at the same time. The outcomes are mutually exclusive; to address this, our options are.
- Run a controlled experiment, where we see some of the potential outcomes with and without treatment.
- Use observational methods, to try to estimate the effect in the absence of a controlled experiment.
- Master time travel.
CausalImpact
What is the CausalImpact approach to this problem?
Building A Model
In order to use the CausalImpact package, we need a few things.
- A time series of our target observation (
Y)- This time series must designate a
pre-periodand apost-periodgroup.
- This time series must designate a
- One more co-variate, “predictor” time-series sets (
X1, andX2), that they themselves are not impacted by the treatment at the time (t). - In a Bayesian Framework, any priors we want include (i.e., from previous studies)
We leverage these co-variate sets to estimate the synthetic-control,
which we use to estimate our causal effect in the post-period.
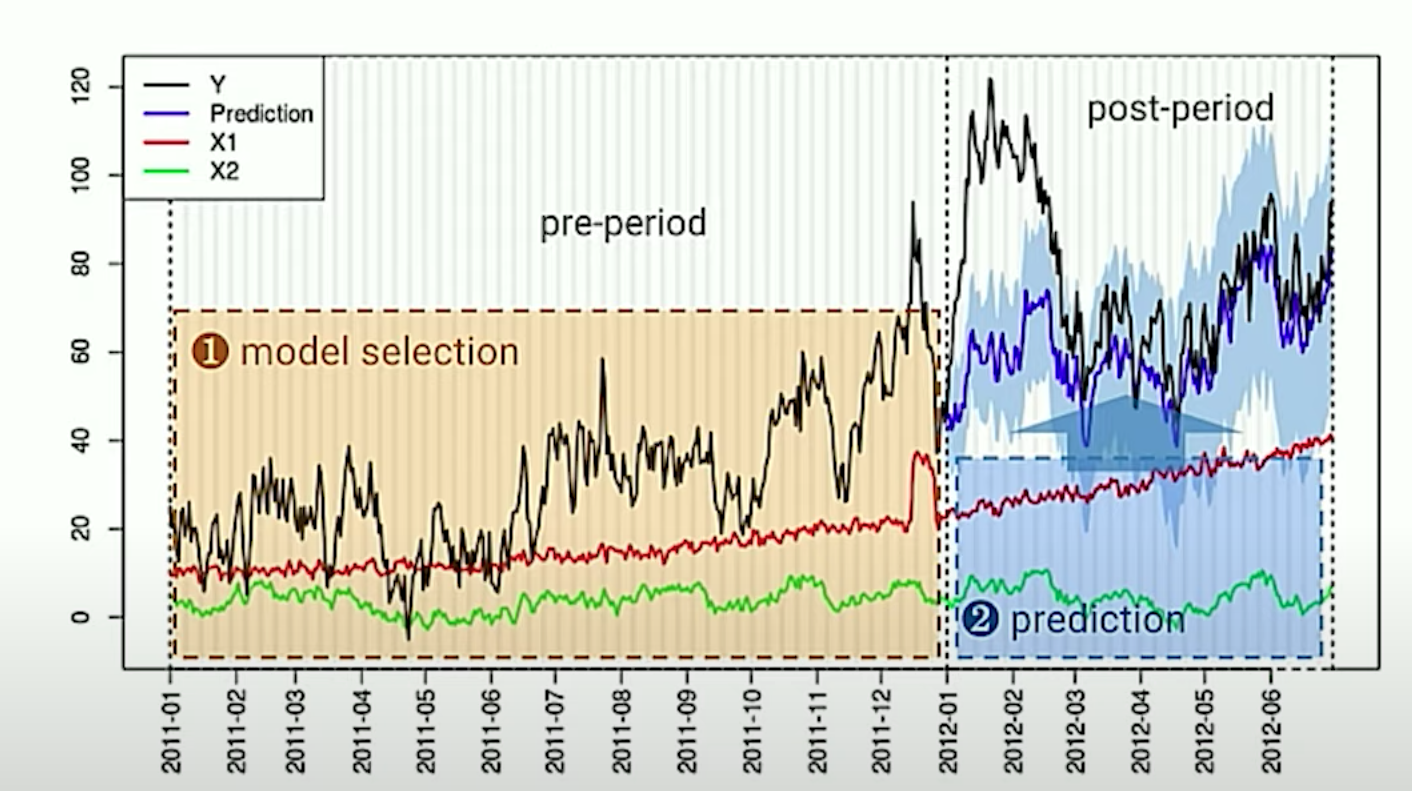 Source:
Youtube - Inferring the effect of an event using CausalImpact by Kay
Brodersen
Source:
Youtube - Inferring the effect of an event using CausalImpact by Kay
Brodersen
Assumptions
It is assumed we have:
- One or more control (
predictor) time series that they themselves are not affected by the intervention - The relationship between the covariates and the treated time series are established during the pre-period, and remain stable in the post period.
A Code
suppressMessages(library(zoo))
suppressMessages(library(CausalImpact))
# <https://google.github.io/CausalImpact/CausalImpact.html>
set.seed(1)
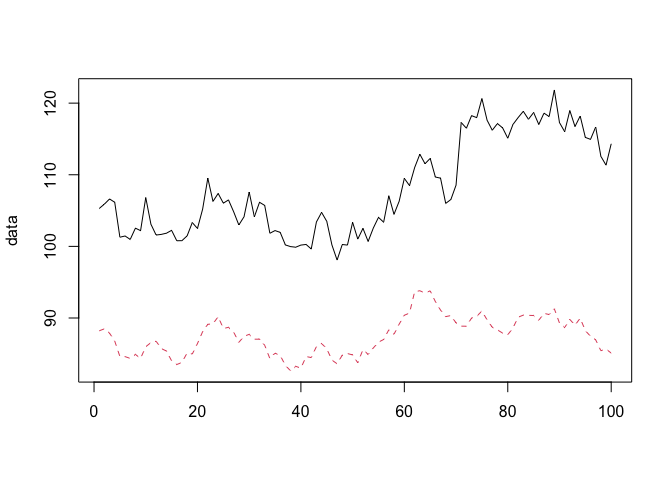
x1 <- 100 + arima.sim(model = list(ar = 0.999), n = 100) # generate covariate series
y <- 1.2 * (x1) + rnorm(100)
y[71:100] <- y[71:100] + 10
time.points <- seq.Date(as.Date("2014-01-01"), by = 1, length.out = 100)
data <- zoo(cbind(y, x1), time.points)
head(data)
## y x1
## 2014-01-01 105.2950 88.21513
## 2014-01-02 105.8943 88.48415
## 2014-01-03 106.6209 87.87684
## 2014-01-04 106.1572 86.77954
## 2014-01-05 101.2812 84.62243
## 2014-01-06 101.4484 84.60650
matplot(data, type = "l")
pre.period <- as.Date(c("2014-01-01", "2014-03-11")) # We need to tell the model what observations occurred prior to treatment
post.period <- as.Date(c("2014-03-12", "2014-04-10")) # We also need to identify the post-treatment period
impact <- CausalImpact(data, pre.period, post.period)
plot(impact)
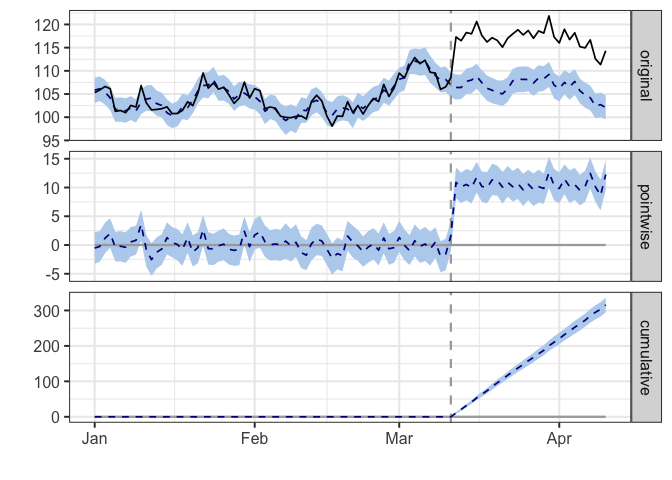
summary(impact)
## Posterior inference {CausalImpact}
##
## Average Cumulative
## Actual 117 3511
## Prediction (s.d.) 107 (0.35) 3196 (10.38)
## 95% CI [106, 107] [3176, 3217]
##
## Absolute effect (s.d.) 11 (0.35) 316 (10.38)
## 95% CI [9.8, 11] [294.4, 336]
##
## Relative effect (s.d.) 9.9% (0.32%) 9.9% (0.32%)
## 95% CI [9.2%, 11%] [9.2%, 11%]
##
## Posterior tail-area probability p: 0.00101
## Posterior prob. of a causal effect: 99.8994%
##
## For more details, type: summary(impact, "report")
Key Questions
Question: How many co-variate (predictor) time series do you need to successfully to this analysis?
Relying on a single co-variate time series runs the risk of reacting quickly to the specifics of the co-variate series. Instead, it is recommended that a handful or a few dozen co-variate time series be used. Enough to guard against spurious correlations, but few that you can understand and explain what each of these time series means.
Source: Youtube - Inferring the effect of an event using CausalImpact by Kay Brodersen @ 26:41
Question: Can you use this method to calculate the impact of multiple events if they overlap in time?
As of 2016, this was an open research question. Need to do additional research to determine if this is still true.
Source: Youtube - Inferring the effect of an event using CausalImpact by Kay Brodersen @ 28:21
Question: The causal impact estimate seems to be at the mercy of the credible intervals. Are tools to analyze and potentially reduce the confidence interval in that post-treatment period?
The confidence interval reflects the uncertainty in our prediction. As you get further out into the future, you are less certain of the output and expect that confidence interval to expand. The better your predictor series are explaining the target, the tighter your confidence intervals are likely to be. The inverse of that, if you don’t have any good predictor time series, then your confidence interval will be wide and reflect that uncertainty.
Source: Youtube - Inferring the effect of an event using CausalImpact by Kay Brodersen @ 28:42
Question: How do we identify ‘good’, covariate predictor time-series?
We want to find time series that are related to our outcome variable, to our original time series, but are not affected by out treatment. Consider a scenario when we launch an advertising campaign for a product. Co-variate time series for this analysis might include queries for the competitor brand, Google Trends data, order volumes for some of your other products, or other time series data that is available during the same period.
Source: Youtube - Inferring the effect of an event using CausalImpact @ 14:02
Key Term(s)
Bayesian Structural Time Series
Statistical technique used for feature selection, time series forecasting, nowcasting, inferring causal impact, and other applications. The model is designed to work with time-series data.
https://en.wikipedia.org/wiki/Bayesian_structural_time_series
Consists of three primary components
- Kalman filter
- Spike-and-Slab
- Bayesian Model Averaging
This is the technique leveraged under-the-hood of CausalImpact package, and available in the bsts R package on CRAN.
Kalman filter
The Kalman filter is an iterative, mathematical process that uses a set of equations and consecutive data inputs to quickly estimate the true value, position, velocity, of the object being measured, when the measured values contain unpredicted or random error, uncertainty or variation.
https://www.youtube.com/watch?v=CaCcOwJPytQ&list=PLX2gX-ftPVXU3oUFNATxGXY90AULiqnWT
More specifically, we can describe the relationship between an
observation at the current time-step x_current as a function of the
previous time step x_previous, some constant a, the current
observation in our system z_current, and a noise measurement at the
current time step v_current.
x_current = a * x_previous z_current = x_current +
v_current
More generally, this translates into
x_current = a * x_previous + v_current
Further research required…
spike-and-slab
Bayesian variable selection technique. Particularly useful when the number of possible predictors is large compared to the number of observations.
https://en.wikipedia.org/wiki/Spike-and-slab_regression
Further research required…
Bayesian model averaging
Ensembling technique for combining Bayesian models.
https://en.wikipedia.org/wiki/Ensemble_learning#Bayesian_model_averaging
Further research required…
counterfactual
Counterfactual conditionals (also subjunctive or X-marked) are conditionals which discuss what would have been true under different circumstances, e.g., “If it was raining right now, then Sally would be inside.” Counterfactuals are characterized grammatically by their use of fake past tense marking, which some languages use in combination with other kinds of morphology, including aspect and mood.
Consider the extension to marketing if we launch an ad campaign and observe the outcome. The counterfactual would be the outcome if we did not launch the campaign.
causal inference
The process of concluding a causal connection based on the conditions of the occurrence of an effect. The main difference between causal inference and inference of association is that the former analyzes the response of the effect variable when the cause is changed.
In this context, it could be thought of as the branch of statistics focused on effects, or the consequences of our actions.
causality
Influence by which one event, process, or state (a cause) contributes to the production of another event, process, or state (an effect) where the cause is partly responsible for the effect, and the effect is partly dependent on the cause.
In simpler terms, B happened because of A.
randomized control trial
A randomized controlled trial (or randomized control trial RCT) is a type of scientific (often medical) experiment that aims to reduce certain sources of bias when testing the effectiveness of new treatments; this is accomplished by randomly allocating subjects to two or more groups, treating them differently, and then comparing them with respect to a measured response
In this example, each group would receive a distinct treatment.
synthetic control
The synthetic control method is a statistical method used to evaluate the effect of an intervention in comparative case studies. It involves the construction of a weighted combination of groups used as controls, to which the treatment group is compared. This comparison is used to estimate what would have happened to the treatment group if it had not received the treatment.
In other words, it is a technique where we generate a control group from existing data points.
Additional Resources:
- Google Blog: CausalImpact: A new open-source package for estimating causal effects in time series
- Google Research: Inferring causal impact using Bayesian structural time-series models
- google/CausalImpact
- YouTube: Inferring the effect of an event using CausalImpact by Kay Brodersen
- Fitting Bayesian structural time series with the bsts R package